This document is a note of learing these two methods.
I also recorded videos about fourier transform and wavelet analysis under my bilibili account.(Fourier Transform, Wavelet Analysis)
What is Fourier Transform
Let’s begin with lights. We know that sunlight seems white but acutally it contain seven colors in that ‘white’ light. By only seeing the white light, I bet there is no one can say what are components in that.
Foutunately, we have prisms. By let the white light going through prisms, it could be automatically separated as different colors. Actually speaking, they are ordered by different frequencies.

There are some many other waves in our life. However, in most sicumstances, we cannot find any pattern in them even if they are repeating regularly. For example, the picture below is a record of sound wave:
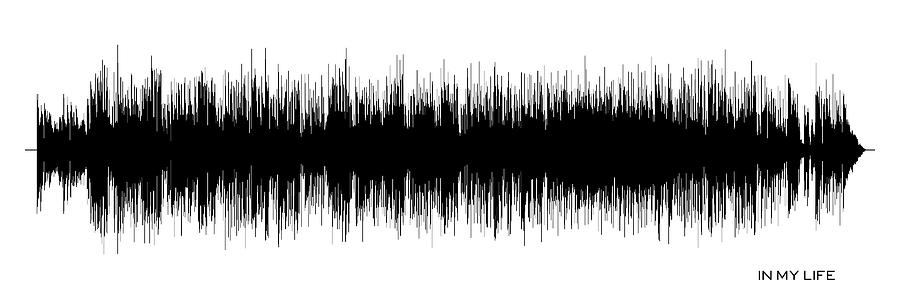
and we cannot tell what different waves in different frequncy composed the wave.
And here comes the fourier transform, it could tell us the proportion of different frequency waves in the complex wave.
Basic Understanding of Fourier Transform
Feel the transformation:
Let’s began with the simplest transforming situation: vector. We know that every vector could be transformed to 2 numbers. For example (1, 2) means the vector from (0, 0) and pointed to the point (1, 2). For every vector, we can transform is as two number. And for any two numbers, we can transform them as a vector.
Same as the waves. Fourier tolds as: every complex waves could be seem as a summary of many sin waves with different frequncy, amplitude, and intercept on x axis. (We do not consider the intercept on y axis because we cannot seperate them.) And we can trasform a wave to three ‘numbers’ (the more formal name is orthogonal basis).
It could be interperted as:
I made a program to let you play with 4 sin curves with any parameters. You may use the following codes in R to open:
1 | library(shiny) |
Calculation of vectors
There is a calculation among vectors called point multiply. For example: (1, 2) point multiplied by (10, 3) equals to 1 10 + 2 3 = 16 and the result is a value. And there is an interesting feature: if two vectors are vertical with each other, the result of point multiply is 0. For example, (10, 1) point multiplied by (-2, 20) is equal to 10 (-2) + 1 20 = 0.
Now, I prepared a question for you. I know there is a vector, but I won’t tell you what is it. If you tell me a vector, I will give you a result of point multiply between your vector and the unknow vector.
In order to find what the unknown vector is, you draw a circle with r = 1 and created vectors with the point on that circle. Then based on the results I give to you, you drawn point on the space:
For example, if you give me (1, 0) and my result is 1.7. Then you would draw a point on the direction of (1, 0) but the distance from (0, 0) is 1.7.
After all, you get a plot like this:
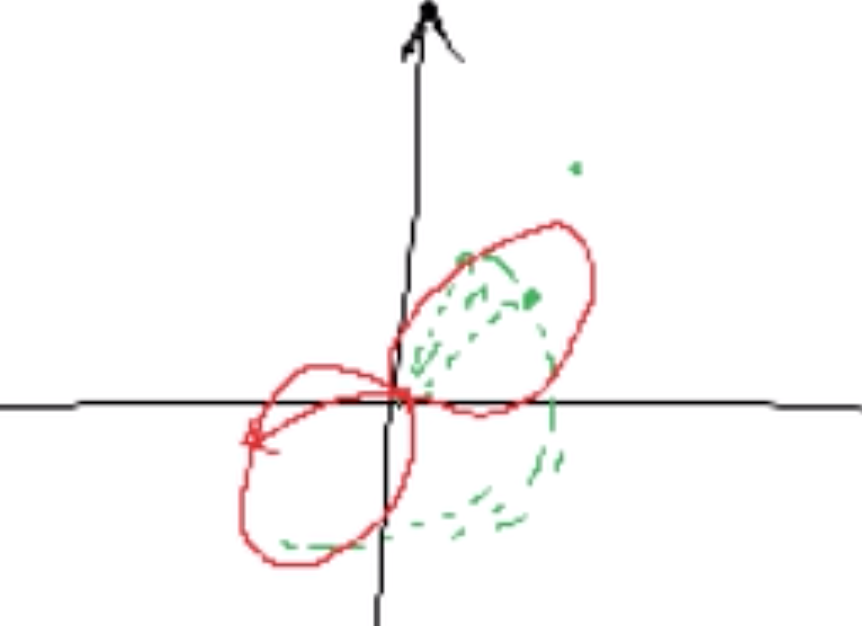
So, can you tell me what is the unknown vector? We can see, in two directions, the result of point multiply is zero. The unknown vector must be on one of the two directions that vertical to the ‘zero-result’ direction!
Same calculation in fourier transform
Same thing as fourier transformation does. We use orthogonal basis of different frequencies to point multiply the complex wave, and we could get result like this:
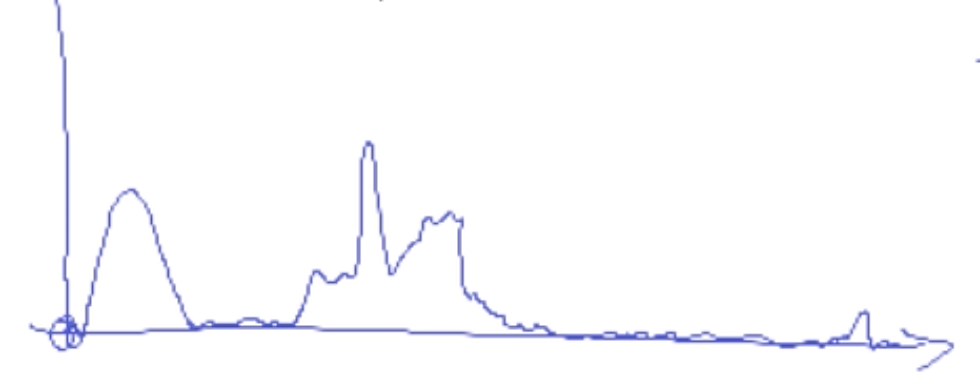
What this plot can tell us? It tells us that this complex wave do know have wave from some frequency because their point multiply is 0 and there are some major frequency in that complex wave whose results of ponit multiply is very high.
This document is unfinished. Later, I will mention how wavelet analysis is a better solution than short period fouries transfrom.
You may also forward to my video to watch this process.